Часть 1 | Часть 2 | Часть 3 | Часть 4 | Часть 5 | Часть 6
Пособие по проектированию жилых зданий. Вып. 3. (к СНиП 2.08.01-85) ПЕРЕКРЫТИЯ Часть 5
|
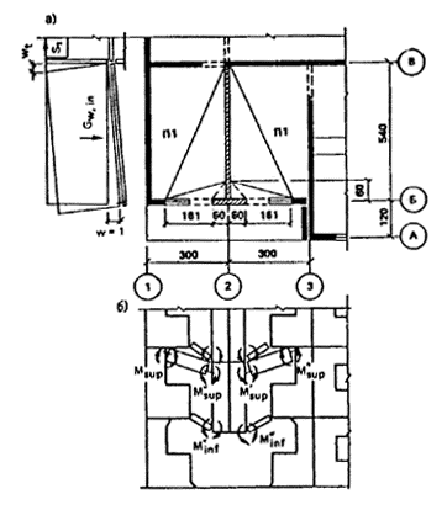
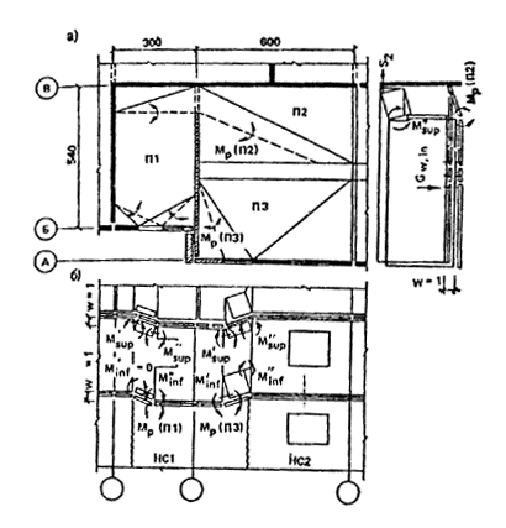
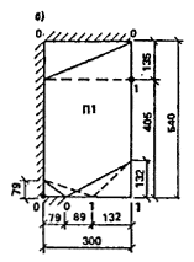
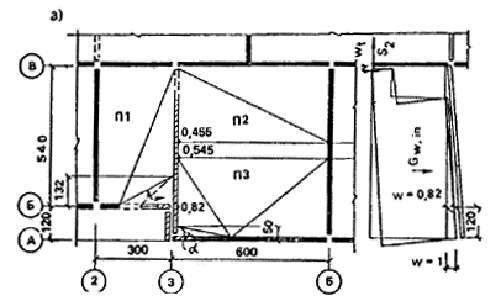
2. Проверка устойчивости здания при локальном разрушении его несущих конструкций по схеме № 1. (рис. 13). Рассматривается обрушение конструктивной ячейки в осях 1 — 3 и Б — В i-го этажа. Первично разрушается панель внутренней стены по оси 2 между осями Б и В и примыкающие к ней простенки панелей наружных стен по оси Б. Проверяется невозможность обрушения зависших над локальным разрушением конструкций перекрытий и стеновых панелей. Прогрессирующему обрушению в данном случае сопротивляются на каждом этаже две плиты П1; связи растяжения второго типа, соединяющие внутреннюю поперечную стену с продольной внутренней стеной; связи сдвига между наружными стенами и внутренней; две наружные стеновые панели, разрушающиеся как рамы с образованием четырех пластических шарниров (см. п. 14).
Рис. 13. 1-я схема излома элементов фрагмента 2.1. Расчет несущей способности отдельных сечений конструктивных элементов. 2.1.1. Панель наружной стены НС1. Расчетное сопротивление материалов определяют по указаниям п. 3 настоящего приложения. Бетон: Rbnyb2yb3/yb = 5,5/1,15 × 1,15 × 1,25 = 6,9 МПа; Rbt = Rbt,nyb2yb3yb = 0,7 × 1,15/1,25 × 1,25 = 0,805 МПа. Арматура диаметром 8 мм класса А-III Rs =390/l,05 × 1,1 = 408 МПа. Верхняя перемычка Несущая способность по изгибу верхней перемычки определяется по СНиП 203.01—84 при Аs = 1,508 см2 (3 стержня диаметром 8 мм из стали класса A-III); b = 35 см; h = 29 см; ho = 29 — 3 = 26 см. Сечение симметричное. Высота сжатой зоны x = (RsAs)/(Rbb) = (408 × 150,8)/(6,9 × 350) = 25,5 мм Несущая способность сечений М1 = М2 = Rbbx(ho 0,5x) = 6,9 × 350 ´ 25,5(260 0,5 × 25,5) = 15,2 × 106 Н×мм = 15,2 кН×м. Невозможность хрупкого разрушения элементов наружной панели проверяется в соответствии с требованиями п. 5. При разрушении наружной стены так, как показано на рис. 13, б, величина поперечной силы, соответствующей возникновению предельных изгибающих моментов в верхней перемычке с коэффициентом 1,5, равна: Q = 1,5(M1 + М2)/lin = 1,5(15,2 + 15,2)/1,61 = 28,3 кН. Поперечное армирование составляют хомуты из 3 стержней диаметром 5 мм из стали класса Вр-1, шаг s = 200 мм: As = 0,59 см2; Rsw = 395/1,2 × 1,1 × 0,8 × 0,9 = 261 МПа. Прочность по наклонной полосе между наклонными трещинами проверяется из условия: Q £ 0,3jw1jb1Rbbh2o mw = Asw/(bs) = 59/(350 ´ 200) = 0,00084; a = Es/Eb = (17 × 104)/(16 × 103) = 10,6; jw1 = 1 + 5amw = 1 + 5 × 10,6 × 0,00084 = 1,04; b = 0,02; jb1 = 1 bRb = 1 0,02 × 6,9 = 0,862; 0,3jw1jb1Rbbho = 0,3 × 1,04 × 0,862 × 6,9 × 350 × 260 = 169 000 Н = 169 кН > 28,3 кН. Условие прочности выполняется. Прочность по наклонной трещине проверяем по условию Q £ Qb + Qsw, где Qb = jb2(1 +jf + jn)Rbtbh2o/c, jb2 = 1,9; jf = 0; jn = 0; (1 + jf + jn) = 1. Проверка производится дважды: для с = 200 мм и для со. с = 200 мм, Qsw = 0; Qb = (l,9 × 0,805 × 350 × 2602)/200 = 180,9 × 103 = 180,9 кН > 28,3 кН. Условие прочности выполняется.
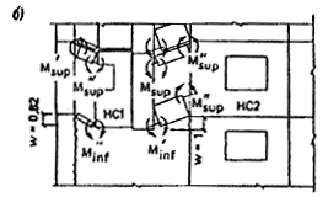
Условие прочности выполняется. Нижняя перемычка Предельные изгибающие моменты для нижней перемычки определяются аналогично. Нижняя арматура 2 стержня диаметром 8 мм из стали класса А-III As = 1,005см2; h = 10 cм; ho = 8см; linf = 0,89 м; М1 = 2,9 кН×м. Верхней арматуры в перемычке нет, M2 = 0. Q = (1,5 × 2,9)/0,89 = 4,9 кН. Поперечная арматура отсутствует. Условие прочности: Q £ jb3 (1 + jn)Rbtbh2o, где jb3 = 0,5; jn = 0; jb3 (1 + jn)Rbtbh2o = 0,5 × l × 0,805 × 350 × 80 × 10-3 = 11,3 кН. 4,9 < 11,3. Условие прочности выполняется. Простенки Несущая способность по изгибу простенков заведомо больше, чем перемычек, так как высота сечения более узкого простенка вдвое больше высоты сечения верхней перемычки при соотношении площадей арматуры 1 : 5. Проверка прочности простенков по поперечной силе дает удовлетворительные результаты и здесь не приводится. Предельные изгибающие моменты, действующие в угловых шарнирах рамы наружной панели НС1, принимаются из расчета перемычек по изгибу: M¢sup = M¢¢sup = 15,2 кН×м; M¢¢inf = 2,9кН×м; M¢¢inf = 0.
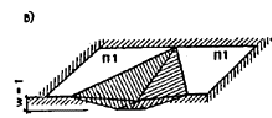
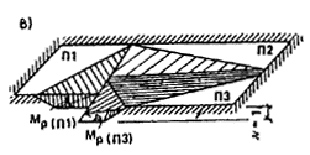
Плиты перекрытий П1 железобетонные (см. табл. 3) размером на комнату, запроектированные на работу при опирании по четырем сторонам, верхней арматуры не имеют, несущая способность их сечений по изгибу при растяжении верхних волокон равна нулю: M¢1 = M¢2 = 0. Несущая способность поперечного сечения плиты П1 по изгибу при растяжении нижних волокон при изгибе вдоль короткой стороны определяется по СНиП 2.03.01—84 при b = 540 см; ho = 14 см; As = 10,05 см2 (20 стержней диаметром 8 мм из стали класса А-III); Rs = 405 МПа, бетон класса В15, Rb = 3,8 МПа и равна M1 = 49,4 кН×м. Несущая способность сечения при изгибе вдоль длинной стороны определяется при b = 300 см, h = 16 см; ho = 14,7 см; Аs = 1,76 см2 (14 стержней диаметром 4 Вр-1), Rs = 370 МПа и равна М2 = 9,7 кН×м. 2.1.3. Несущая способность связей. а) Связи сдвига третьего типа в конструкции отсутствуют, то есть S3 = 0. б) Связь растяжения второго типа между внутренними стенами состоит из двух стержней диаметром 12 мм из стали класса А-I (Ast = 2,26 см2) с расчетным сопротивлением Rs = 235/1,1 × 1,1 = 235 МПа. Несущая способность связи S2 = 235 × 226 = 53110 Н = 53,1 кН. 2.2. Оценка возможности возникновения механизма прогрессирующего обрушения первого типа. Поскольку плиты перекрытий заведены в стены, а внутренняя поперечная стена не имеет дверного проема, первый механизм обрушения невозможен (см. п. 8 настоящего приложения). 2.3. Оценка возможности возникновения механизма прогрессирующего обрушения второго типа. Расчет производится в соответствии с пп. 9 (см. рис. 13), 13 — 15 настоящего приложения. 2.3.1. Анализ сопротивления наружных стен. Поскольку в данном примере рассматривается здание с наружными стенами из железобетонных панелей, в соответствии с указаниями п. 14, расчет следует начинать с оценки сопротивления, прогрессирующему обрушению панелей наружных стен и лишь после этого переходить к проверке возможности образования различных типов механизмов прогрессирующего обрушения, изложенной в пп. 8 — 11. Оценка сопротивления наружных стеновых панелей прогрессирующему обрушению производится по формулам (22), (23). Слева и справа одинаковые панели НС 1, их разрушение одинаково, предельные изгибающие моменты приняты по п. 2.1.1: M¢sup = M¢¢sup = 15,2 кН×м; M¢inf = 2,9кН×м; M¢¢inf = 0; lsup = 1,61 м; linf = 0,89 м; w = 1. Работа внутренних сил определяется по формуле (23): W'w,ex = W¢¢w,ex = (15,2 × 2/1,61 + 2,9/0,89)1 = 22,1 кН, Ww,ex = 2 × 22,l = 2 кH. Работа сил веса определяется по формуле (11) при G¢w,ex = G¢¢w,ex = 26,6 кН; Uw,ex = 2 × 0,5 × 26,6 × 1 = 26,6 кН. Проверяется условие (25): Rw,ex = Ww,ex Uw,ex > 0, Rw,ex = 44,2 — 26,6 = 17,6 кН > 0. Условие выполнено. 2.3.2. Сопротивление обрушению плит перекрытий. Плиты перекрытий заведены в наружные стены, поэтому для них определяется сопротивление их внешнего края по п. 15. Левая и правая плиты одинаковы, схемы излома их также одинаковы и показаны на рис. 13, в. Изгибающие моменты, воспринимаемые сечениями плиты П1, принимаются по п. 2.1.2: M¢1 = M¢2 = 0; М1 = 49,4 кН×м; М2 = 9,7 кН×м. Сопротивление внешнего края плиты перекрытия, заведенного в наружные стены, подсчитывается по формуле (29) настоящего приложения, которая в случае M¢1 = M¢2 = 0 принимает вид WIIpi,bor = si(M1i/Li + M2i/li)wi/di, тогда при s1 = s2 = 0,6 м и d1 = d2 = l,61 м для каждой плиты получим: WIIp1,bor = WIIp2,bor = 0,6/1,61(49,4/5,4 + 9,7/3) × = 4,6 кН; WIIp,bor = WIIp1,bor + WIIp2,bor = 2 × 4,6 = 9,2 кH. Теперь по формуле (27) определяем Uw,ex = Rw,ex Wp,bor = 17,6 9,2 = 26,8 кН×м и далее весь расчет производится в соответствии с требованиями п. 9. Работа внутренних и внешних сил на перемещениях плит перекрытий подсчитывается по формулам (15): WIIp = WIIp1 = WIIp2 = 0 при М'11
= М¢12 =
М'21 = М'22 = 0;
2.3.3. Работа связей определяется по формуле (13), которая при S3 = 0 примет вид: WIIt = S2y2/L. В п. 2.1.3 определено S2 = 53,l кН; y2 = 2,6 м (высота стены); L = 5,4 м; WIIt = 53,1 × 2,6/5,4 = 25,5 кН. 2.3.4. Работа поперечной внутренней стены. Панель внутренней стены поворачивается как жесткий диск, при этом работа сил веса определяется по формуле (14) UIIw,in = Gw,inx/L + G1, где Gw,in = 54,9 кН; G1 = 2,2 кН; x = 0,5L; UIIw,in = 54,9 × 0,5 + 2,2 = 29,7 кН. 2.3.5. Проверка общего условия невозможности образования механизма второго типа. Проверка производится по формуле (12) WIIt + WIIр > UIIw,in + UIIр + Uw,ex; WIIt + WIIр = 25,5 кН; UIIw,in + UIIр + Uр,ex = 29,7 + 25 26,8 = 27,9 кН > 25,5 кН. Условие равновесия не выполняется. Необходимо или усилить связь второго типа, или поставить связи третьего типа. В последнем случае необходимая несущая способность связей с учетом формулы (13) определяется S3 = (27,9 — 25,5)L/h = (2,4 × 5,4)/ 2,6 = 5 кН, что соответствует площади сечения стержня из стали А-I As = 5 × 10/235 = 0,21 см2. 2.4. Оценка возможности возникновения механизма прогрессирующего обрушения третьего типа. Проверка производится в соответствии с п. 10. Для третьего механизма обрушения рассматривается обрушение одних только плит перекрытий, расположенных непосредственно над выбитыми панелями, защемление плит в этих панелях не реализуется и в соответствии с требованиями п. 15 настоящего приложения в формулах (16) и (17) нужно принимать Uw,ex S4wwex = 0. Тогда формула (16) примет вид: WIIр ³ UIIр, где WIIр = 0, UIIр = 25 кН (см. п. 2.3.2). Условие (16) не выполняется (0 < 25), следовательно, необходимо установить связи растяжения между плитой и вышерасположенной стеной. При установке на внешнем углу каждой плиты связи диаметром 10 мм из стали класса А-I получим S5 = 18,4 кН, x5 = L, w = 1. Тогда проверяется условие (17), которое при WIIр = 0 и Uw,ex S4wwex = 0 запишется WIIIt ³ UIIр, где WIIIt = nS5x5w/L = 2 × 18,4 = 36,8 кН > 25 кН, условие необрушения соблюдается. 2.5. Оценка возможности возникновения механизма прогрессирующего обрушения четвертого типа. Так как внутренняя поперечная стена не имеет проемов, а плиты перекрытий заведены в стены, этот механизм обрушения невозможен (см. п. 11). 3. Проверка устойчивости здания при локальном разрушении его несущих конструкций по схеме № 2. Рассматривается обрушение конструктивной ячейки в осях 2 — 5 и А — В (рис. 14) на i-м этаже здания. Первично разрушается панель внутренней стены по оси 3 между осями А и В и примыкающие к ней два простенка наружных стен по осям А и Б. Проверяется невозможность обрушения зависших над этим локальным разрушением конструкций перекрытий и стеновых панелей. Прогрессирующему разрушению в данном случае сопротивляются на каждом этаже панель внутренней стены; связи сдвига и растяжения, соединяющие ее с внутренними продольными стенами; плиты перекрытий слева и справа от оси 3; наружные стены и связи сдвига между наружными стенами и панелью внутренней стены.
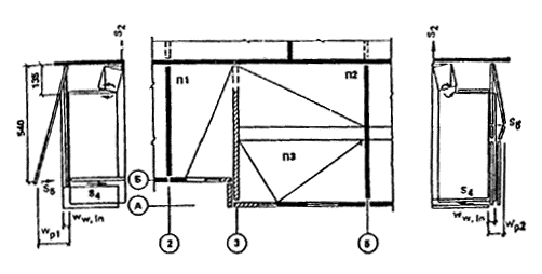
Рис. 14. 2-я схема излома элементов фрагмента 3.1. Расчет несущей способности отдельных сечений конструктивных элементов. 3.1.1. Панель наружной стены НС1. Несущие способности сечений панели при изломе ее (как рамы с четырьмя пластическими шарнирами) примем по результатам расчета, приведенного в п. 2.1.1: M¢sup = M¢¢sup = 15,2 кН×м; M'inf = 2,9 кН×м; M¢'inf = 0. 3.1.2. Панель наружной стены НС2. Панель двухмодульная, при потере одной опоры работает как рама с образованием четырех пластических шарниров. Предельные изгибающие моменты в сечениях верхней перемычки. При Rb = 12,6 МПа; Rs = 405 МПа; Аs = 1,01 см2; b = 35 см, h = 46 см определяют по аналогии с перемычками панели НС1, и равны М1 = М2 = 17,3 кН×м. Предельные изгибающие моменты в сечениях подоконной перемычки при Аs = 1,01 см2; b = 35 см, h = 87 см, равны М1 = М2 = 34,5 кН×м. Несущая способность простенков по изгибу заведомо больше, чем перемычек, так как при одинаковом с перемычкой армировании они имеют большую высоту сечения. Проверка возможности разрушения панели от действия поперечной силы производится так, как это показано в расчете панели НС1. Здесь этот расчет не приводится, он дает удовлетворительный результат. Предельные изгибающие моменты, действующие в угловых шарнирах рамы, равны M¢w,sup = M¢¢w,sup = 17,3 = 17,3 кН×м; M¢w,inf = M¢¢w,inf = 34,5 кН×м. 3.1.3. Плиты перекрытий. Предельные моменты в сечениях плиты П1 принимаются из расчета, приведенного в п. 2.1.2: М¢11 = М¢21 = 0; М11 = 49,4 кн×м; М21 = 9,7 кН×м. Плита перекрытия П2 не имеет верхней арматуры, следовательно М'12 = М¢22 = 0. При характеристиках h = 16 см, бетон класса М20, Rb = 18,8 МПа определяют несущие способности сечений. Изгиб вдоль короткой стороны: b = L = 600 см, ho = 14,5 см, Аs = 6,09 см2 (31 стержень диаметром 5мм из проволоки класса Вр-I); Rs = 362 МПа, M12 = 32,l кH×м. Изгиб вдоль длинной стороны: b = l = 300 см; ho = 13 см; As = 35,41 см2 (23 стержня диаметром 14 мм из стали класса А-III); Rs = 405 МПа; М22 = 150,4 кН×м. Плита перекрытия П3 по размерам, классу бетона, высоте сечения и армированию аналогична плите П2, следовательно несущие способности по изгибу ее сечений равны M¢13 = М¢23 = 0; М13 = 32,1 кН×м; М23 = 150,4 кН×м. 3.1.4. Панель внутренней стены. Прочность по изгибу сечения перемычки — «флажка» определяется по аналогии с сечениями перемычек наружных стен при характеристиках: h = 52,5 см; Rb = 13,8 МПа; b = 16 см; Аs = 1,508 см2, Rs = 405 МПа. Предельный изгибающий момент М¢¢sup = 29,7 кН×м. Прочность сдвиговой связи S1 определяется по рекомендациям п. 5.36 и формуле (124). Пособия: S1 = hfrRsAs,tr, где hfr = 0,7; Rs = 235 МПа, As,tr = 2,260 cм2 (2 стержня диаметром 12 мм из стали класса А-I), S1 = 0,7 × 235 × 226 × 10-3 = 37,2 кН. Далее проверяется условие (6) S1 > l,5 М¢¢suр/b, l,5 М¢¢suр/b = l,5 × 29,7/1,35 = 33 кН < 37,2 кН, условие удовлетворяется. Прочность горизонтальной связи растяжения определяет прочность левого опорного сечения перемычки. Рассмотренная в предыдущем пункте связь при работе на растяжение имеет прочность S2 = 235 × 0,226 = 53 кН. Сопротивление изгибу левого сечения перемычки М¢suр = S2ho = 53(52,5 — 1,5) = =27 кН×м. Здесь принимается, что прочность анкеровки связи и прочность примыкающей стены не менее прочности связи на растяжение. Нижняя перемычка в проеме отсутствует и М'inf = М'¢inf = 0. 3.1.5. Связи сдвига четвертого типа Эти связи соединяют наружные панели с внутренней стеной. Прочность каждой связи определяется по аналогии со связью сдвига S1, при As,tr = 1,13 см2; S4 = 0,7 × 235 × 0,113 = 18,6 кН. 3.2. Оценка возможности возникновения механизма прогрессирующего обрушения первого типа (см. рис. 14). Расчет производится в соответствии с п. 8 и с учетом пп. 13 — 15. 3.2.1. Анализ сопротивления наружных стен. а) Схема разрушения левой панели НС1 отличается от описанной в 2.3.1 только величиной рабочего пролета надоконной перемычки. При расположении балконной двери ближе к обрушаемой внутренней стене, чем окно lsup = linf = 0,89 м. Предельные изгибающие моменты приняты по п. 2.1.1 M¢sup = M¢¢inf = 15,2кН×м; M¢inf = 0; M¢¢inf = 2,9 кН×м. По формуле (23) вычисляем W¢w,ex = (5,2 × 2/0,89 + 2,9/0,89) 1 = 37,4 кН. б) Наружная панель НС2 имеет оконный проем, где lsup = linf = 0,91 м; предельные моменты приняты по п. 3.1.2 M¢sup = M¢¢sup = 17,3 кH×м; M¢inf = M¢¢inf = 34,5 кН×м; w = 1; по аналогии с НС1 вычисляется: W¢¢w,ex = (2 × 17,3 + 2 × 34,5)/0,91 = 113,8 кН. в) Сумма работ внутренних сил наружных панелей вычисляется по формуле (22) Ww,ex = W¢w,ex + W¢¢w,ex = 151,2 кН. Работа сил веса наружных стен определяется по формуле (11) п. 8, но так как панель НС2 двухмодульная, в формулу подставляется не полный вес панели, а половина его. Тогда: Uw,ex = 0,5(G¢w,ex + 0,5G¢¢w,ex) = 0,5(26,6 + 0,5×68,7) = 30,5 кН. Затем проверяется условие (25) Rw,ex = WW,ex — Uw,ex > 0. Rw,ex = 113,8 — 30,5 = 83,3 кН > 0, условие выполнено. 3.2.2. Сопротивление обрушению плит перекрытий. а) Левая плита перекрытий имеет характеристики: М¢11 = M¢21 = 0; М11 = = 49,4 кН×м; М21 = 9,7 кН×м; L = 5,4 м; t = 1,35 м; f = 0. Для первого механизма обрушения сопротивление внешнего края определяется по формуле (28), которая в случае М¢11 = M¢21 = 0 принимает вид:
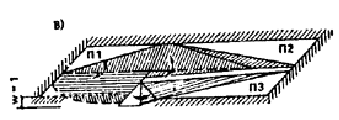
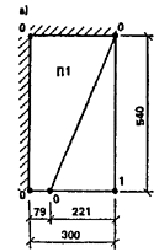
Здесь s = 1,32 м; d = 0,89; е = 0,79 м (рис. 15, б). Работа внутренних и внешних сил на перемещениях плиты перекрытия П1 подсчитывается по формуле (9) при М¢11 = M¢21 = 0 WIp1 = M21/t = 97/1,35 = 7,2 кН; UIp1 = 0,5ql(L 2/3t) = 0,5 × 6,3 × 3(5,4 2/3 ´ 1,35) = 42,5 кН. б) Плита перекрытия П2 (см. рис. 15, в, г).
Так как в. прил. 2 не рассматривается случай разрезки перекрытия в
комнате на две и более плит, работа внутренних и внешних сил
определяется по формулам п. 6
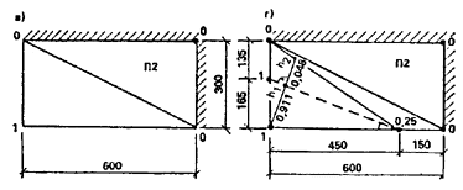
Схема излома плиты П2 показана на рис. 15, г, пунктиром обозначен пластический шарнир с растяжением нижней арматуры. Направление этого шарнира выбрано таким, чтобы работа внутренних сил была минимальной. Из геометрических соотношений находим h1 = 1,55 м; h2 = 1,03 м; а = 20,1°. Угол перелома плиты в пластическом шарнире w = (0,911 — 0,048)/1,03 — (1 — 0,911)/1,55 = 0,781 1/м.
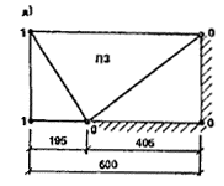
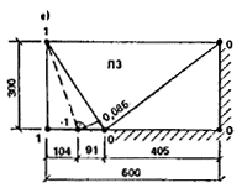
Рис. 15. Возможные схемы излома плит перекрытий Предельный изгибающий момент в сечении по линии шарнира М = M12a1cos a/L + M22a2sin a/l = 32,l/6 × 4,5 × cos 20,l° + 150,4/3 × 1,65 × sin 20,1° = 53,4 кН×м. WIp2 = Mw = 53,4 × 0,781 = 41,7 кН. UIp2 = 1/6 × 6,3[[4,5 × l,65(l + 1 + 0,25) + 1,5 × 3(0 + 0 + 0,25) + l,35 × 4,5(0 + l+ 0,25)] = 26,7 кН. в) Плита перекрытия П3 (см. рис. 15, д, е). Армирование плиты П3 аналогично плите П2. Несущая способность поперечных сечений плиты по изгибу M13 = 32,1 кН×м; М23 = 150,4 кН×м. Пластические шарниры проходят через края оконного проема в наружной стене (рис. 15, е). Пластический шарнир с растяжением нижних волокон возникает в плите из-за ее защемления в наружных стенах, поэтому работа внутренних сил на перемещениях этого шарнира относится к сопротивлению внешнего края. Из геометрических соотношений h = 0,787 м; w = 1,161/м; а = 70,9°. Так же, как и для плиты П2, вычисляется M = 144 кН×м, а также величины WIp3,bor и UIp3 WIp3,bor = Mw = 144 × 1,16 = 167 кН; UIp3 = 34,5 кН×м. г) Величина Wp4 для доборной плиты равна нулю, работа внешних сил определяется UIp4 = 0,5qLl = 0,5 × 6,3 × 6 × 0,6 = 11,3 кН. д) Суммируя по всем плитам перекрытия ячейки, получим WIp,bor = WIp1,bor + WIp3,bor = 16.4 + 167 = 183,4 кН, WIp = WIp1 + WIp2 = 7,2 + 41,7 = 48,9 кН, UIp = UIp1 + UIp2 + UIp3 + UIp4 = 42,5 + 26,7 + 34,5 + 11,3 = 115 кН. В соответствии с указаниями п. 15 по формуле (27) определяется UIw,ex = RIw,ex WIp,bor = 83,3 183,4 = 266,7 кН. 3.2.3. Работа поперечной внутренней стены. Предельные моменты в перемычке — «флажке» (см. п. 3.1.4 Пособия) М¢sup = 27 кН×м; М¢¢sup = 37,2 кН×м. При отсутствии нижней перемычки М¢inf = М¢¢inf = 0, и тогда формула (5) примет вид WIw,inf = (M¢sup + M¢¢sup)/b = (27 + 29,7)/1,35 = 42 кН. Вес панели Gw,in = 55,5 кН. Нагрузка, передающаяся с лоджии Cl = 14 + 0,6 × 1,2 × 3 × 1/2 = 15,1 кН, где вес стенки лоджии составляет 14 кН. Работа внешних сил на единичном перемещении вычислим по формуле (7) UIw,in = 70,6 кН. 3.2.4. Проверка общего условия невозможности образования механизма первого типа. Проверка производится по формуле (4), которую в случае отрицательного значения Uw,ex запишем в виде WIw,in + WIp Uw,ex ³ UIw,in + UIp. Подставляя в эту формулу полученные выше значения, получим 42 + 48,9 + 266,7 > 70,6 + 115; 357,6 > 185,6, условие выполняется, обрушение конструкций по рассматриваемой схеме (механизм I типа) невозможно. 3.3. Оценка возможности возникновения механизма прогрессирующего обрушения второго типа (рис. 16). Расчет производится в соответствии с требованиями п. 9 и с учетом пп. 13 — 15, а также особенностей конструкции рассматриваемой ячейки.
Рис. 16. 3-я схема излома элементов фрагмента 3.3.1. Анализ сопротивления наружных стен. Схемы излома наружных керамзитобетонных стен те же, что и для первого механизма обрушения с той только разницей, что перемещение левой панели НС1 равно w¢¢ = w¢¢L¢/L¢¢ = l × 5,4/6,6 = 0,82. Тогда, используя результат, полученный в п. 3.2.1а, определяем: W¢w,ex = 37,4 × 0,82 = 30,7 кН. Для правой наружной панели w = 1, значит, как и в п. 3.2.1б W¢w,ex = 113,8 кН; W¢w,ex = 30,7 + 113,8 = 144,5 кН. При подсчете работы сил веса, учитывая, что перемещение НС1 w1 = 0,82, получим Uw,ex = 0,5(26,6 × 0,82 + 0,5 × 68,7) = 28,l кН; Rw,ex = 144,5 — 28,1 = 116,4 кН > 0. 3.3.2. Сопротивление обрушению плит перекрытий. а) Сопротивление внешнего края левой плиты П1 определяется по формуле (29), которая при М¢11 = М¢21 = 0 имеет вид WIIp,bor = s/d(M11/L + M21/l)w¢ = 1,32/0,89 (49,4/5,4 + 9,7/3) 0,82 = 15,1 кН. Работа внутренних и внешних сил, приложенных к плите П1, принимается из расчета, изложенного в п. 2.3.2, при w = 0,82, WIIp1 = 0; UIIp2 = 0,82 × 12,5 = 10,2 кН. б) Плита П2 разрушается с образованием одного пластического шарнира с растяжением верхних волокон (см. рис. 16). Так как верхней арматуры в плите нет, WIIp2 = 0. UIIp2 = l/6 × 6,3 × 3 × 6 × 0,455 = 8,6 кН. в) Разрушение плиты П3 показано на рис. 16, г, пластический шарнир с растяжением нижних волокон определяет сопротивление внешнего края перекрытия, заведенного в наружную стену. Из геометрических соотношений определяют величины w = 1,42 1/м, и а = 37,5°. Предельный изгибающий момент, воспринимаемый сечением плиты по линии пластического шарнира, подсчитывается по формуле, приведенной в п. 3.2.2б и равен М = 16,4 кН. Тогда работы внешних и внутренних сил, приложенных к плите П3, составят: WIIp3,bor = 42,3 кН; WIIp3 = 0; UIIp3 = 10 кН. г) Работа внешних сил на перемещениях доборной плиты UIIp4 = 0,5(0,455 +0 ,545)0,5 × 6,0 × 6,3 × 0,6 = 5,7 кН. д) Сумма работ внутренних сил в плитах перекрытий ячейки составит WIIp,bor = 15,1 + 42,3 = 57,4 кН; WIIp = 0; UIIp = 10,2 + 8,6 + 10 + 5,7 = 34,5 кН. По формуле (27) определяем UIIw,ex = Rw,ex WIIp,bor = 116,4 57,4 = 173,8 кН. 3.3.3. Работа связей. Связей сдвига третьего типа между перекрытием и нижерасположенной внутренней стеной в конструкции нет, поэтому формула (13) принимает вид WIIt = S2y2/L, где S2 = 53 кН; y2 = 2,6 м; L = 6,6 м; WIIt = 20,9 кН. 3.3.4. Сопротивление внутренней стены. Работа внешних сил, приложенных к внутренней поперечной стене, вычисляется по формуле (14) при Gw,in = 55,5 кН; Gt = 15,l кН, L = 6,6 м; х = [15,14 × 2,6(1,35 + 0,5 × 5,14) + 0,5 × 0,525 × 1,352]/(5,14 × 2,6 + 1,35 × 0,525) = 3,75 м. UIIw,in = Gw,inx/L + Gt = 55,5 (3,75/6,6) + 15,l = 46,6 кН. 3.3.6. Проверка общего условия невозможности образования механизма второго типа. Проверка производится по формуле (12). которую в данном случае удобнее записать в виде WIIt Uw,ex ³ UIIw,in + UIIp; 26,9 + 173,8 > 46,6 + 34,5; 200,7 кН > 81,1 кН, условие выполняется. Обрушение конструкций по рассматриваемой схеме (механизм второго типа) невозможно. 3.4. Оценка возможности возникновения механизма прогрессирующего обрушения третьего типа. Как указывалось в п. 2.4, проверку устойчивости к прогрессирующему обрушению в данном случае нужно вести по формуле WIIIp ³ UIIIр. В связи с тем. что перекрытие справа разрезано на три плиты, схемы разрушения этих плит отличаются от схем, описанных в прил. 2, поэтому условие (16) проверяется отдельно для каждой плиты. а) Обрушение плиты П1 (см. рис. 15, а) рассмотрено в п. 2.4, проведенный расчет показал необходимость установки связи диаметром 10 мм прикрепляющей угол плиты к вышерасположенной стене. б) Схема обрушения плиты П2 показана на рис. 15, в. Возникновение пластического шарнира в плите с растяжением верхней арматуры не вызывает работы внутренних сил из-за отсутствия верхней арматуры, то есть WIIIp2 = 0. Работа внешних сил на перемещениях плиты UIIIp2 = 1/6 qLl = 18,9 кН. Условие устойчивости против обрушения WIIIp ³ UIIIp не выполняется, так как 0 < 18,9 и, следовательно, необходимо угол плиты прикрепить связью к вышерасположенной стене. При установке стержня диаметром 10 мм из стали класса А-I получаем n = 1; S5 = 18,4 кН; x5 = L, и тогда по формуле (17) проверяется условие необрушения плиты П2: WIIIt2 > UIIIp2, где WIIIt2 = 18,4 кН. Таким образом, 18,4 кН » 18,9 кН, связь достаточна. в) Аналогичным образом определяется необходимость установки связей пятого типа 2 стержня диаметром 10 мм из стали класса А-I в плите П3; схема излома которой показана на рис. 15, д. Определив величины работ внутренних и внешних сил на перемещениях плиты П3: WIIIp3 = 0; UIIIp3 = 31,2 кН, WIIIt3 = 2 × 18,4 = 36,8 кН, проверяем условие невозможности обрушения: WIIIt3 = 36б8 кН > 31,2 кН, условие выполняется. 3.5. Проверка общего условия невозможности образования механизма четвертого типа. 3.5.1. Анализ сопротивления наружных стен. По указанию п. 15 настоящего приложения необходимо проверить условие Stw > Rw,ex. Так как связи растяжения седьмого типа между наружными стенами и плитами перекрытий отсутствуют в конструкции, Stw = 0, и упомянутое условие не выполняется; в соответствии с п. 15 в формуле (19) нужно принимать Uw,ex = 0, ww,ex = 0. 3.5.2. Работа плит перекрытий. В связи с тем, что левое перекрытие разрезано на отдельные плиты, величины WIVp и UIVp вычисляют в соответствии со схемами излома элементов, показанными на рис. 17.
Рис. 17. 4-я схема излома элементов фрагмента Все плиты перекрытий разрушаются с образованием верхних пластических шарниров, следовательно WIVp = 0. Для подсчета работ внешних сил, приложенных к плитам перекрытий, из очевидных геометрических соотношений определяют их перемещения wp1 = 1; wp2 = (0,25 × 3)/1,35 = 0,56; wp3 = ww,in = 0,25. Далее определяют работу внешних сил на перемещениях каждой плиты перекрытия: Up1 = 6,3 × 5,4 × 2,21 × l/6 = 12,5 кН; Up2 = 6,3 × 3 × 6 × 0,56/6 = 10,6 кН; Up3 = 6,3(3 × 6 × 0,25 + l,95 × 3 × 2 × 0,25)/6 = 7,8 кН; Up4 = 0,5 × 6,3 × 0,6 × 6 × 0,5(0,25 + 0,56) = 3,2 кН; UIVp = 12,5 + 10,6 + 7,8 + 3,2 = 34,1 кН. 3.5.3. Работа связей. а) Сопротивление связей пятого типа (см. п. 3.4) S5 = 18,4 кН. Связи шестого типа в конструкции отсутствуют.
Работа внутренних сил при разрушении связей определяется по
формуле (20)
б) Связи сдвига четвертого типа в конструкции представлены тремя стержнями диаметром 12 мм из стали класса А-I по одному стержню между внутренней стеной и каждой наружной панелью, а также между стенкой лоджии и внутренней стеной, несущая способность каждого стержня в соответствии с п. 3.1.5 равна 18,6 кН, тогда S4 = 18,6 × 3 = 55,8 кН. Сопротивление внутренней стены Из п. 3.2.3 принимается WIw,in = 42 кН; UIw,in = 70,6 кН. 3.5.4. Проверка общего условия невозможности образования механизма четвертого типа. Проверка производится по формуле (19), которая в случае равенства нулю величин WIVp, Uw,ex и ww,ex, принимает вид (1 с/L)WIw,in + WIVt ³ (1 с/L)UIVp + UIVp S4ww,in, где L = 5,4 м; L — c = 1,35; 1 с/L = 0,25. Подставляя вычисленные выше значения, получим (1 с/L)WIw,in + WIVt = 0,25 × 42 + 19,5 = 30 кН; (1 с/L)UIw,in + UIVp S4ww,in = 0,25 × 70,6 + 34,1 55,8 × 0,25 = 37,7 кН >30 кН. Условие необрушения не выполняется, рекомендуется поставить связи шестого типа, несущая способность которых с учетом формулы (20) определяется S6 = L/(L — с) × (37,7 — 30) = 30,8 кН. Обеспечить величину S6 можно, например, поставив два стержня диаметром 10 мм из стали класса А-I. ПРИЛОЖЕНИЕ 3 РАСЧЕТ КОНСТРУКЦИЙ НИЖНИХ НЕЖИЛЫХ ЭТАЖЕЙ БЕСКАРКАСНЫХ ЖИЛЫХ ЗДАНИЙ 1. В настоящем приложении рассмотрены особенности расчета сборных несущих конструкций нижних нежилых этажей жилых зданий, конструктивные решения которых рекомендованы разд. 2 настоящего Пособия. 2. Несущую систему конструкций нижних нежилых этажей рекомендуется рассчитывать совместно с опирающимися на них конструкциями верхних этажей. При расчете здания допускается из несущей системы выделять фрагмент, состоящий из конструкций подвала, техподполья, первого нежилого этажа, технического этажа и типового жилого этажа либо двух типовых этажей, по верху которых приложена нагрузка от веса конструкций вышерасположенных этажей и ветровая нагрузка на них. При расчете зданий комбинированной системы с каркасными нижними этажами горизонтальные (ветровые) нагрузки рекомендуется передавать на стены лестнично-лифтовых узлов. При расчете зданий стеновой системы со встроенными нежилыми нижними этажами допускается в первом приближении усилия от горизонтальных нагрузок определять как для регулярной системы без учета изменения положения и размеров проемов в нижних этажах. После определения усилий от горизонтальной нагрузки каждая из стен (диафрагм жесткости) рассчитывается с учетом реальной схемы и расположения проемов. При расчете рекомендуется учитывать, что для зданий высотой 12 этажей и менее, как правило, усилия от ветровых нагрузок не являются определяющим для назначения сечений конструкций и их армирования. Поэтому компоновку несущей системы зданий со встроенными нежилыми помещениями допускается выполнять исходя из вертикальных нагрузок. 3. Несущую систему конструкций нижних этажей рекомендуется рассчитывать с использованием метода конечного элемента (МКЭ). Расчет допускается выполнять в упругой стадии. При использовании МКЭ рекомендуется: модель разбивать на прямоугольные элементы так, чтобы размеры простенков и перемычки были кратны размерам сетки; при арочных проемах дуги окружности заменять прямыми и вводить в углах треугольные плоские элементы; платформенный стык моделировать в виде прямоугольных элементов с толщиной, равной средней толщине верхней и нижней панелей и модулем упругости, который является обратной величиной от податливости платформенного стыка на сжатие; стойки каркаса моделировать связями конечной жесткости, которые учитывают также податливость основания; в плоскую расчетную модель необходимо включать горизонтальные связи между конструкциями, расположенными вдоль одной оси, которые работают в нижнем этаже на растяжение, а выше — на сжатие, с их реальными жесткостными характеристиками; при расчете стеновых систем в расчетной схеме необходимо учитывать податливость основания; в зданиях с опиранием перекрытий по трем и четырем сторонам рекомендуется пользоваться для расчета пространственными расчетными схемами с включением стен поперечного и продольного направлений, учитывая связи на сдвиг конечной жесткости (между продольной и поперечной стеной) в уровне перекрытий, это позволит снизить нагрузку на простенок поперечной стены в уровне пола второго этажа, примыкающий к продольной стене, на 10 — 15 % в зависимости от конструкции; при наличии оси симметрии в расчет включать часть поперечника до оси симметрии, учитывая работу отрезанной части выполнением краевых условий на оси симметрии. 4. Прочность конструкций встроенных этажей и их армирование рекомендуется проверять по интегральным значениям усилий в основных сечениях, полученным исходя из напряжений в этих сечениях. 5. При расчете зданий стеновой системы принимается, что основными сечениями, по которым необходима проверка прочности, являются горизонтальные опорные сечения в уровне пола первого и второго этажей, горизонтальные сечения по верху проемов и вертикальные сечения перемычек первого этажа в местах заделки и в середине пролета; горизонтальные стыки необходимо проверять на действие вертикального давления, перемычку — на растяжение в центре и поперечную силу в заделке, а также момента. 6. При назначении размеров и расположения проемов в первом этаже следует учитывать, что несимметричное расположение проема в первом этаже приводит к неравномерному распределению давления в зоне платформенного стыка; наиболее выгодно располагать проем в первом этаже симметрично так, чтобы проем в типовом этаже находился в зоне перемычки над проемом первого этажа. 7. Размеры простенков в панели первого этажа должны назначаться таким образом, чтобы среднее давление на 1 м простенка не превышало несущей способности 1 м платформенного стыка, при этом в расчетную длину шва над панелью первого этажа могут быть включены участки перемычек длиной 0,5 от ее высоты в месте заделки в простенок. При несимметричном расположении проемов наиболее нагружен меньший по ширине простенок (как правило). 8. Расчет перемычки на действие поперечной и внецентренной продольной сил можно выполнять независимо. Для назначения размеров сечения поперечную силу в перемычке рекомендуется определять как произведение максимального среднего давления на 1 м простенка, умноженного на 0,8 высоты перемычки. Растягивающая сила в перемычке может быть определена как усилие в затяжке условной арки. Для перемычек пролетом от 3,3 до 2,4 м такая условная арка (рис. 1) приближенно имеет пролет, равный пролету перемычки в свету, и высоту, также равную пролету перемычки; растягивающее усилие в ней рекомендуется определять по формуле
где q — нагрузка от верхних этажей в уровне пола второго типового этажа; lo — пролет перемычки в свету; hlin — высота перемычки; hmin — минимальная высота перемычки, равная 0,5м.
Рис. 1. Схема условной арки для определения растягивающей силы в перемычке первого нежилого этажа 9. Если по результатам упругого расчета расчетные параметры конструкции определяют усилия сжатия в горизонтальном стыке, то данные упругого расчета могут быть использованы для определения прочности и армирования конструкции. Если определяющими являются усилия в перемычке, то рекомендуется применить для расчета упругую расчетную модель, позволяющую снизить расход арматуры на армирование перемычки. 10. Для бескаркасных зданий, в одном панельном нежилом этаже которых стеновые панели имеют большие (более 1,5 м) проемы, допускается приближенный расчет перемычек и стыков стеновых панелей при выполнении следующих конструктивных ограничений: длина панели — не менее 6 м, ширина проема — не более 2,4 м, ширина каждого из простенков — не менее 0,75 от ширины проема, высота сечения перемычки — не менее 1/3 от ее длины (ширины проема), в панели технического подполья проемы расположены под проемом нежилого этажа. Число панелей с большими проемами не превышает трех на каждую секцию. Если перечисленные ограничения соблюдены, то прочность верхнего стыка и перемычки панели нежилого этажа проверяется по следующим формулам: при отсутствии проема в стеновой панели жилой части дома
при наличии в жилом этаже проема, расположенного в плане в пределах проема нежилого этажа и имеющего ширину, меньшую половины ширины проема нежилого этажа (см. рис. 1):
В формулах (2) — (5) N — равнодействующая всех внутренних вертикальных усилий в уровне верха стеновой панели нежилого этажа; Rj1 — предельное сопротивление стыка над панелью нежилого этажа; t1, t2 — толщины стеновых панелей жилого и нежилого этажей соответственно; M1, М2 — предельные моменты, воспринимаемые сечениями перемычки на опоре и в середине пролета, вычисляемые по СНиП 2.03.01—84; l1, l2 — ширины простенков панели нежилого этажа; Rbt — расчетное сопротивление бетона при растяжении; ho — рабочая высота сечения перемычки; qsw — усилие в хомутах на единицу длины перемычки; lnt — длина панели жилого этажа за вычетом ширины проема (lnt = lw1 l01). При подборе поперечной арматуры перемычки должно быть соблюдено условие
где Rb — расчетное сопротивление бетона при сжатии, jw1 и jb1 — коэффициенты, вычисляемые по СНиП 2.03.01—84. Прочность нижнего стыка оценивается по формулам: для левого простенка N (1 + 0,5l02/l1)/lwi £ 0,8Rj2t2; (7) для правого простенка N (1 + 0,5l02/l2)/lwi £ 0,8Rj2t2, (8) где Rj2 — предельное сопротивление стыка под панелью нежилого этажа. 11. При каркасном решении нижних этажей здания наиболее напряженными участками балок-стенок, которые необходимо проверять расчетом, являются следующие: перемычки (верхние и нижние) в зоне проемов (для прохода людей); они должны быть проверены на поперечную силу и момент, действующие в этом сечении; участки главных балок-стенок в местах опирания на них второстепенных балок-стенок необходимо проверять на действие поперечной силы и смятие опорных частей; опорные участки балок-стенок и колонн рассчитывать на смятие. 12. Прогибы балок-стенок, на которые опираются несущие стены здания при каркасной конструкции нижних этажей, рекомендуется ограничивать исходя из предельных взаимных смещений стеновых панелей, равных 1 см. Предельные прогибы ригелей следует принимать по СНиП 2.03.01—84. 13. Для увеличения несущей способности и жесткости системы возможно объединение балок-стенок и ригелей в единую систему при помощи металлических или железобетонных связей по длине зоны контакта. Несущая система балки-стенки и ригеля может считаться монолитной, если стыковое соединение воспринимает сдвигающее усилие равное или большее, чем усилие, определяемое по формуле Т = (М — Мb — Мr)/Н, (9) где М — максимальный момент внешних сил, действующий на систему; Мb, Мr — предельные моменты, воспринимаемые балкой-стенкой и ригелем; Н — расстояние между нейтральными осями балки-стенки и ригеля. В случае, если условие (9) не выполняется для систем, в которых жесткость ригеля соизмерима с жесткостью балки-стенки, несущую способность системы можно проверять методом предельного равновесия. Несущая способность системы должна определяться как наименьшее из значений, соответствующих различным нормальным сечениям, наиболее опасными из которых являются: в середине пролета системы, в зоне проема, в местах изменения высоты, толщины сечения и армирования. 14. Для системы, предельное состояние которой определяется образованием шарнира в зоне максимального момента, предельную нагрузку на систему можно определить по формуле
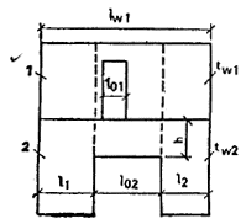
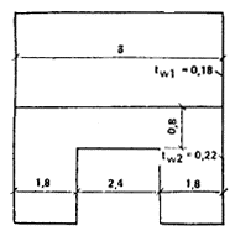
где q — равномерно распределенная нагрузка, проложенная по верху балки-стенки и соответствующая несущей способности системы по рассматриваемому нормальному сечению; Мb, Мr — предельные моменты, воспринимаемые балкой-стенкой и ригелем в рассматриваемом сечении; М¢b — момент в рассматриваемом сечении несущего элемента от нагрузки, приложенной непосредственно к элементу (включая собственный вес балки-стенки); М¢b = qol1(l l1)/2; (11) l — расчетный пролет системы, определяемый по формуле l = lo + (c1 + c2)/3; (12) lo — пролет в свету между опорами; с1, с2 —ширина левой и правой площадок опирания; l1 — расстояние до рассматриваемого сечения; Т1, T2 — предельные сдвигающие силы, воспринимаемые стыком на участках l1 и (l — l1). 15. Расчетную длину колонн (при их расчете на вертикальную нагрузку) рекомендуется принимать в зависимости от жесткости узлов между балками-стенками и колонной, жесткости дисков перекрытий и наличия диафрагм жесткости, но не менее высоты первого этажа. В местах опирания ригелей на колонны необходимо предусмотреть металлические закладные детали в колонне и ригеле, воспринимающие часть опорного момента, величиной не менее 30 кН×м. Пример расчета. Требуется проверить прочность стеновой панели первого нежилого этажа, показанной на рис. 2 (lw = 6 м).
Рис. 2. Стеновая панель первого нежилого этажа Исходные данные: N = 3400 кН. Бетон класса В20 Rb = 11,5 МПа, Rbt = 0,9 МПа. Арматура класса А-III Rs = 355 МПа, Rsw = 255 МПа. Армирование в опорных и пролетном сечениях перемычки одинаково, площадь сечения продольной арматуры As = 942 мм2. Площадь сечения хомутов Asw = 85 мм2. Шаг хомутов s =150 мм. Прочность стыков: верхнего Rj1 = 4,5 МПа, нижнего Rj2 = 6,5 МПа. Толщины панелей: жилого этажа tw1 = 180 мм; нежилого этажа tw2 = 220 мм. Высота перемычки h = 800 мм; ho = 760 мм. Предельные моменты сечения перемычки: M1 = M2 = M. Высота сжатой зоны х = (355 × 942)/(11,5 × 220) = 132 мм. Относительная высота сжатой зоны: x = 132/760 = 0,174 < xR = 0,625. Предельный момент поперечного сечения М = 11,5 × 220 × 7602 × 0,174(1 0,5 × 174) = 253 × 106 Н×мм. Проверка выполнения неравенства (2):
Усилие в хомутах на единицу длины перемычки qsw = 255 × 85/150 = 144 Н/мм. Проверка выполнения неравенства (3):
Для проверки выполнения неравенства (6) вычисляем jw1 = l + 5 × 20 × 104/(24 × 103)85/(220 × 150) = 1,108; тогда jb1 = 1 — 0,01 × 11,5 = 0,885;
Проверка прочности нижнего стыка по формуле (8): 3400000/6000 [1 + 0,5(2400/1800)] = 944 < 0,8 × 6,5 × 220 = 1140 Н/мм. Кроме проверки прочности необходимо проверить ширину раскрытия трещин. ПРИЛОЖЕНИЕ 4 РЕКОМЕНДАЦИИ ПО ОПРЕДЕЛЕНИЮ ПОДАТЛИВОСТИ СОЕДИНЕНИЙ ЭЛЕМЕНТОВ НЕСУЩИХ КОНСТРУКЦИЙ 1. В настоящем приложении приведены рекомендации по определению коэффициентов податливости соединений сборных бетонных и железобетонных элементов, а также швов бетонирования стен из монолитного бетона, стыков между сборными и монолитными конструкциями жилых зданий и перемычек. Коэффициентом податливости соединения называется величина, численно равная деформации соединения, вызванной единичной сосредоточенной или распределенной силой. Коэффициенты податливости соединений при растяжении lt, сдвиге lt, коэффициенты податливости перемычек при перекосе ltin определяют от сосредоточенных сил; коэффициенты податливости при сжатии lс и повороте lj — от распределенных сил. Для соединений, имеющих несколько характерных стадий работы (например, до образования трещин в соединении и после), коэффициенты податливости (жесткости) следует принимать для каждой стадии дифференцированно. Деформация соединения в этом случае определяется как сумма деформаций от приращений усилий на отдельных этапах. Основные виды соединений и размерность коэффициентов податливости приведены в табл. 1. Таблица 1
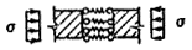
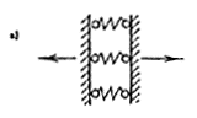
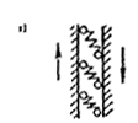
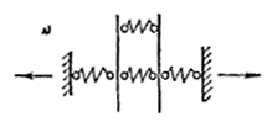
При соединении элементов системой связей следует различать следующие случаи их расположения: последовательное (рис. 1, а, б); параллельное (рис. 1, в, г); смешанное (рис. 1, д, е).
Рис. 1. Схема соединений а, б — последовательные; в, г — параллельные; д, е — смешанные последовательное (рис. 1, а, б); параллельное (рис. 1, в, а); смешанное (рис. 1, д, е). Коэффициенты податливости l соединения, состоящего из системы сосредоточенных связей, определяют по формулам: в случае последовательного расположения связей
в случае параллельного расположения связей
где n — число связей в соединении; li — коэффициент податливости i-й связи. В смешанном случае выделяют группы однородно расположенных связей и для каждой из них по формулам (1) или (2) вычисляют коэффициенты податливости, в результате чего систему приводят к случаю последовательного или параллельного расположения связей. Для определения коэффициента податливости соединения, имеющего сосредоточенные и распределенные связи, последние заменяют эквивалентными по жесткости, сосредоточенными. 2. Коэффициент податливости при растяжении lt соединения сборных элементов в виде сваренных между собой и замоноличенных бетоном арматурных выпусков определяют по формуле lt = 2aсrс/ss, (3) где acrc — ширина раскрытия трещин, нормальных к арматурной связи, вызванных растягивающими напряжениями в связи ss; значение ширины раскрытия трещин рекомендуется определять по указаниям норм проектирования железобетонных конструкций. Деформации растяжения связей в виде петлевых выпусков диаметра 8 — 12 мм, соединенных между собой скобами из арматурной стали и замоноличенных бетоном класса не ниже В 15, можно определять как для сварных связей, площадь которых соответствует площади поперечного сечения арматуры петлевого выпуска. Диаметр арматуры скобы должен быть при этом не менее диаметра петлевого выпуска. 3. Коэффициент податливости при сжатии соединения элементов определяют в зависимости от конструктивного типа стыка. Для контактного горизонтального стыка, в котором сжимающую нагрузку передают через слой раствора, толщиной не более 30 мм, коэффициент податливости при сжатии lс,соn определяют по формуле lс,соn = (lт + hcon/Eb,w)А/Асoп, (4) где lт — коэффициент податливости горизонтального растворного шва при сжатии, определяемый по п. 4 настоящего приложения; hcon —высота контактного участка стыка; Eb,w —модуль деформации бетона стены; А — площадь горизонтального сечения стены в уровне расположения проемов; Асoп — площадь контактного участка стыка, через которую передают сжимающую нагрузку. Для монолитного горизонтального стыка, в котором сжимающая нагрузка передается через растворный шов в уровне верха перекрытия и слой бетона, коэффициент податливости при сжатии Ас,топ определяют по формуле lс,топ = (lm + lтоп + hтоп/Eтоп)A/Aтоп, (5) где hmon — высота (толщина) слоя монолитного бетона в стыке; Eтоп —начальный модуль упругости бетона замоноличивания стыка; Атoп — площадь монолитного участка стыка (за минусом опорных участков перекрытий и других ослаблений сечения стыка); lтоп — коэффициент податливости, вычисляемый по п. 5 настоящего приложения. Для платформенного горизонтального стыка, в котором сжимающая нагрузка передается через опорные участки плит перекрытий и два растворных шва, уложенные между плитами перекрытий и соединяемыми элементами, коэффициент податливости при сжатии lc,pl определяют по формуле lc,pl = (l¢m + l¢¢m + hpl/Epl)A/Apl, (6) где l¢m, l¢¢m — коэффициенты податливости при сжатии соответственно верхнего и нижнего растворных швов; hpl — высота (толщина) опорной части плиты перекрытия; Epl — начальный модуль упругости бетона опорной части плиты перекрытий; Apl —площадь платформенных участков стыка, через которые передается сжимающее усилие; при неодинаковых размерах опорных площадок вверху и внизу плиты перекрытия принимается их среднее значение. Для платформенно-монолитного стыка, в котором сжимающая нагрузка передается через платформенный участок площадью Apl и монолитный участок площадью Атoп, коэффициент податливости при сжатии A c,pl,mon определяют по формуле lc,pl,mon = l/(1/lc,pl + l/lc,mon), (7) где lc,mon, lc,pl — коэффициенты податливости при сжатии, вычисляемые соответственно по формулам (5) и (6). Для контактно-платформенного стыка, в котором сжимающая нагрузка передается через контактный участок площадью Асoп и платформенный участок площадью Apl, коэффициент податливости при сжатии lс,соп,pl вычисляют по формуле lс,соп,pl = 1/(1/lс,соn + 1/lc,pl), (8) где lс,соn, lc,pl — коэффициенты податливости при сжатии, вычисляемые соответственно по формулам (4) и (6). 4. Коэффициент податливости при сжатии горизонтального растворного шва lm определяют в зависимости от способа укладки и прочности раствора и среднего значения сжимающих напряжений в растворном шве sm. При кратковременном сжатии для раствора прочностью на сжатие 1 МПа и более при толщине шва 10 — 20 мм коэффициент податливости растворного шва lm рекомендуется определять по формулам при sm £ 1,15R2/3m; lm = 1,5 × 10-3 R-2/3mtm; (9) при sm ³ 1,15R2/3m, но не более 2R2/3m; lm = 5 × 10-3 R-2/3mtm; (10) где sm — среднее значение сжимающих напряжений в растворном шве, МПа; Rm — кубиковая прочность раствора, МПа; tm — толщина растворного шва, мм; lm — коэффициент податливости растворного шва при кратковременном сжатии, мм3/Н. Коэффициенты податливости растворных швов при кратковременном сжатии при расчете на нагрузки, действующие в стадии эксплуатации здания, разрешается принимать по табл. 2. Таблица 2
Для горизонтальных швов бетонирования стен из монолитного бетона классов В7,5 — В15 коэффициент податливости при сжатии принимается равным: для тяжелого бетона 0,01 мм3/Н(1 × 10-4 см3/кгс); для легкого бетона 0,02 мм3/Н (2 × 10-4 см3/кгс). При сжатии горизонтального растворного шва или шва бетонирования стены из монолитного бетона длительной нагрузкой коэффициент податливости разрешается вычислять по формуле lm,t = lm(l + jt), (11) где lm — коэффициент податливости шва при кратковременном сжатии; jt — характеристика ползучести шва, принимается равной 1.
| ||||||||||||||||||||||||||||||||||||||||||||
Часть 1 | Часть 2 | Часть 3 | Часть 4 | Часть 5 | Часть 6
Хотите оперативно узнавать о новых публикациях нормативных документов на портале? Подпишитесь на рассылку новостей!

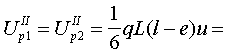
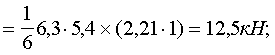
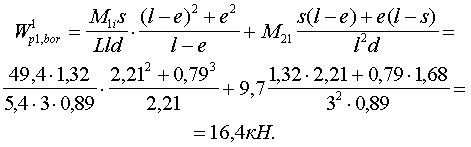
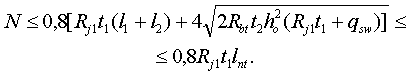 (3)
(3)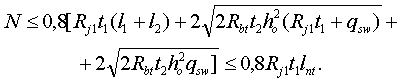 (5)
(5)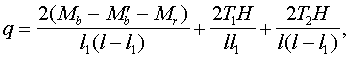 (10)
(10)
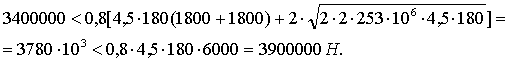
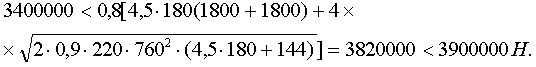
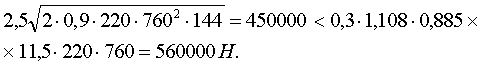
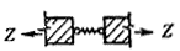


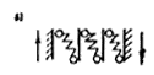
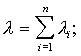 (1)
(1)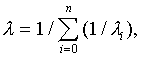 (2)
(2)